算法原理
本算法脱胎于固体退火,对于物理模型不做过多解释,通过下图来理解。
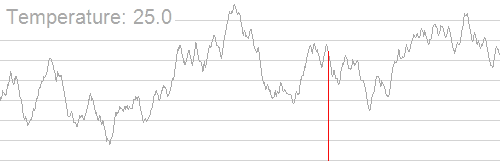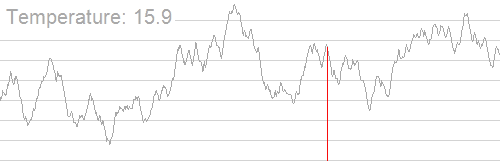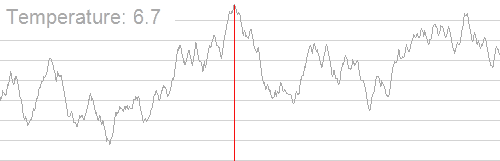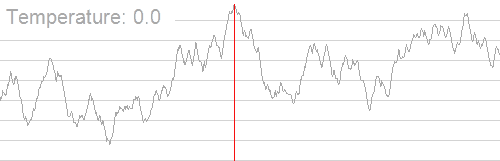
调参方法
通常有以下几种调参的方式:
- 调大初温 T0
- 调小末温 Tk
- 调大温度变动量Δ。
- 选取一个新的随机数种子。
srand(time(0)); - 多跑几遍模拟退火。
开O2
加粗的是最有用的两种
算法实现
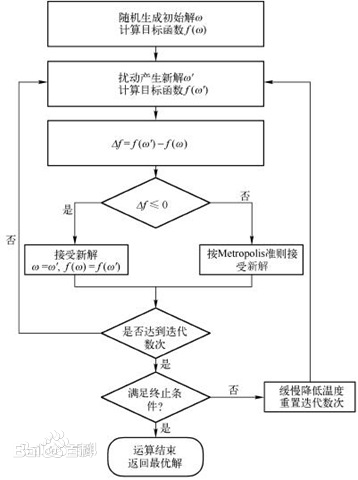
代码实现
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#include<ctime>
using namespace std;
const double delta=0.996;
const double eps=1e-15;//这个参数看人品
const int maxn=1e4+7;
struct node
{
int x,y,w;
} T[maxn];
double ansx,ansy,answ;
int n;
double energy(double x,double y)//根据题目进行修改
{
double res=0,dx,dy;
for(int i=1; i<=n; ++i)
{
dx=x-T[i].x;
dy=y-T[i].y;
res+=sqrt(dx*dx+dy*dy)*T[i].w;
}
return res;
}
void simulate_anneal()//模板部分
{
double t=3000;
while(t>eps)//略大于0
{
double ex=ansx+(rand()*2-RAND_MAX)*t;//随机生成新的答案
double ey=ansy+(rand()*2-RAND_MAX)*t;//随机生成新的答案
double ew=energy(ex,ey);//随机生成新的答案
double de=ew-answ;
if(de<0)
{
ansx=ex;
ansy=ey;
answ=ew;
}
else if(exp(-de/t)*RAND_MAX>rand()) //以Metropolis接受准则 来进行概率接受,求最大值用小于,求最大值用大于
{
ansx=ex;
ansy=ey;
}
t*=delta;
}
}
void solve()
{
simulate_anneal();
simulate_anneal();
simulate_anneal();
simulate_anneal();
}
int main()
{
//srand(time(0));
cin>>n;
for(int i=1; i<=n; ++i)
{
cin>>T[i].x>>T[i].y>>T[i].w;
ansx+=T[i].x;
ansy+=T[i].y;
}
ansx/=n;
ansy/=n;
answ=energy(ansx,ansy);
solve();
printf("%.3lf %.3lf\n",ansx,ansy);//华丽的输出
return 0;
}

