前置知识
强连通分量(SCC)
算法原理
通过 DFS 把该有向图当中的一个子图作为一颗树来进行搜索,把每一个没有被搜索过的点入栈,回溯时判断栈顶到栈底的节点是不是一个强连通分量。
时间复杂度:O(N+M)
算法演示
DFN[i]:DFS 的顺序
LOW[i]:表示 i 通过非父子关系所能够回到的节点中最小的 LOW[i]
判断方法:参见算法图解第 3 步
idx[i]:表示强连通分量的序号(可以用染色来理解)
当遍历到的节点满足
DFN[i]=LOW[i]时,从栈底取出,直到取完 i 节点为止,取出节点组成强连通分量
算法图解
从节点1 开始 DFS,把遍历到的节点加入栈中。搜索到节点 u=6时,无路可走,开始回退。此时,DFN[6]=LOW[6],找到了一个强连通分量,{6} 为一个强连通分量。
此时每一个新入栈的节点,其下一个节点均不存在于栈中,则 LOW[i]=DFN[i]

此时,DFN[5]=LOW[5],找到了一个强连通分量,{5} 为一个强连通分量。
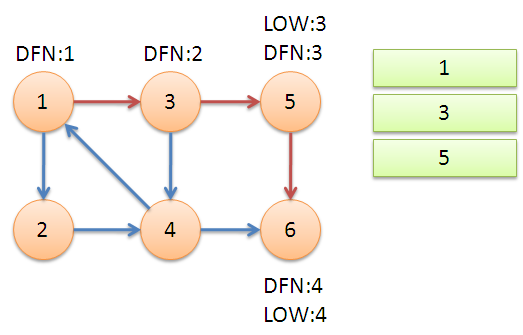
此时节点 3 还有剩余的边可以进行搜索,搜索到节点 1 时发现,节点 1 已经在栈中,则意味着 {1,3,4} 构成一个回路,即 {1,3,4} 为一个强连通分量,即
LOW[1]=LOW[3]=LOW[4]=1。算法的要求是对未搜索过的点进行入栈,由于此时节点 6 已经搜索过,则跳过 4->6这条边
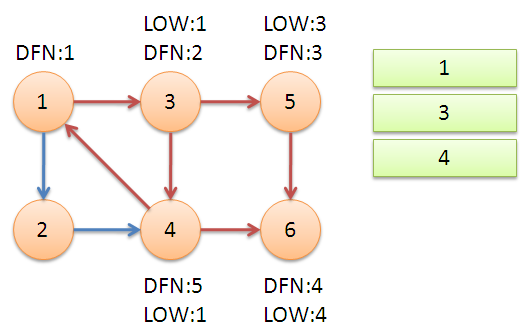
继续回到节点 1,最后访问节点 2。访问边 2->4,结点 4 还在栈中,所以 LOW[2]=DFN[4]=5,返回1后,发现 DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
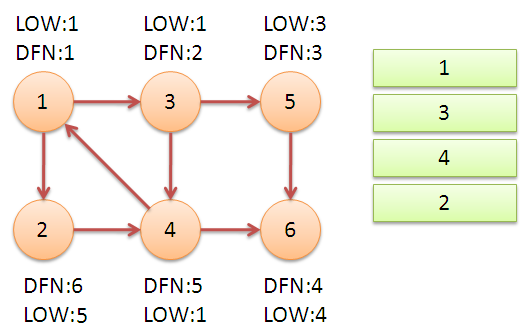
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
struct Edge
{
int v,next;
} E[8010];
int T[3010];
int Head[3010],idx[3010],num,num_Edge,depth;
int N,M,P,Ans=0;
int in[3010],V[3010];
//vector<int>Path,Root;
vector<int>S;
void Add_Edge(int from,int v)
{
++num_Edge;
E[num_Edge].next=Head[from];
E[num_Edge].v=v;
Head[from]=num_Edge;
}
int DFN[3010],LOW[3010];
bool vis[3010];
void Tarjan(int x)
{
DFN[x]=LOW[x]=++num;
S.push_back(x);//此节点未被搜索过,入栈
vis[x]=true;//此节点在栈中
for(int i=Head[x]; i; i=E[i].next)
{
int v=E[i].v;
if(DFN[v]==-1)//下一个节点未搜索
{
Tarjan(v);
LOW[x]=min(LOW[v],LOW[x]);//在不通过父子关系 回溯的情况下,所能取到的最小LOW
}
else if(vis[v])
{
LOW[x]=min(LOW[v],LOW[x]);//在不通过父子关系 回溯的情况下,所能取到的最小LOW
}
}
if(LOW[x]==DFN[x])//构成强连通分量
{
++depth;//第几个强连通分量
while(S.back()!=x)
{
idx[S.back()]=depth;
vis[S.back()]=false;//出栈
V[depth]=min(V[depth],T[S.back()]);
S.pop_back();
}
idx[S.back()]=depth;
vis[S.back()]=false;//出栈
V[depth]=min(V[depth],T[S.back()]);
S.pop_back();
}
}
int main(void)
{
memset(idx,-1,sizeof(idx));
memset(DFN,-1,sizeof(DFN));
scanf("%d",&N);
scanf("%d",&P);
for(int i=1; i<=N; ++i) V[i]=1e9+7,T[i]=1e9+7;
for(int i=1; i<=P; ++i)
{
int t;
scanf("%d",&t );
scanf("%d",&T[t]);
}
scanf("%d",&M);
for(int i=1; i<=M; ++i)
{
int u,v;
scanf("%d%d",&u,&v);
Add_Edge(u,v);
}
for(int i=1; i<=N; ++i)
if( DFN[i]==-1&&T[i]!=1e9+7) Tarjan(i);//Gabow(i);
for(int i=1; i<=N; ++i)
{
if(DFN[i]==-1)
{
printf("NO\n%d",i);
return 0;
}
}
for(int i=1; i<=depth; ++i) in[i]=true;
for(int i=1; i<=N; ++i)
for(int j=Head[i]; j; j=E[j].next)
if(idx[i]!=idx[E[j].v]) in[idx[E[j].v]]=false;
for(int i=1; i<=depth; ++i)
if(in[i]&&V[i]!=1e9+7) Ans+=V[i];
printf("YES\n%d",Ans);
return 0;
}

