三分法

本文转载自算法学习笔记(62): 三分法，并进行一定修改

原理

以求极大值为例，每次对一个区间[l,r]求三等分点lsec和rsec：

• 如果f(lsec) < f(rsec) ，说明极大值一定在[lsec,r]内取到，因为如果在[0,lsec)内，那rsec一定处于单调下降的区间内，它的函数值不可能大于lsec的函数值。 于是我们令l=lsec并继续。

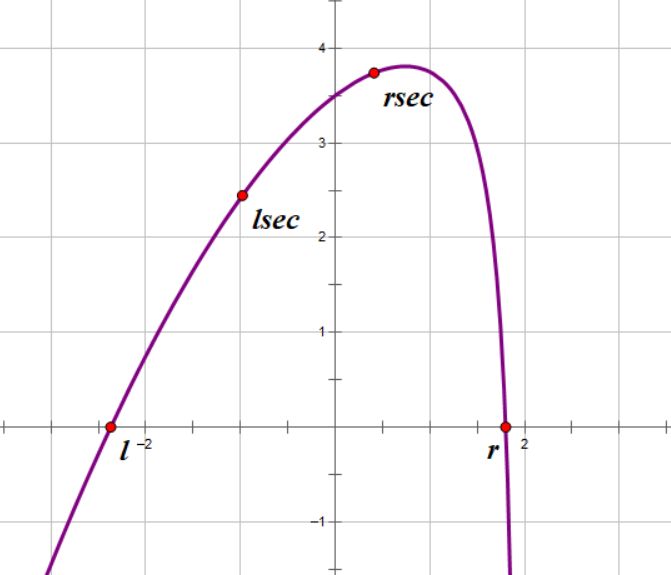
• 如果f(lsec) > f(rsec)，同理，极大值一定在[l,rsec]内取到，令r=rsec并继续。

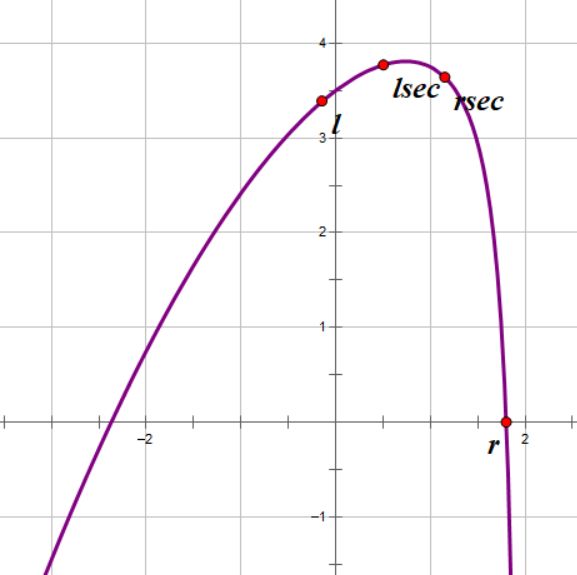
这样进行下去，直到l和r的差距小于设定的 eps 为止。如果求的是极小值而非极大值，只需把上面条件判断处的大于、小于互换。

按照上面的算法，我们每次减少三分之一的长度。但其实还可以优化，即每次在中点附近取点，那么每次可以减少约二分之一的长度。

代码实现（优化版）

while (r - l > eps)
{
    mid = (l + r) / 2;
    double fl = f(mid - eps), fr = f(mid + eps);
    if (fl < fr)//求最小值把小于换成大于
        l = mid; // 这里不写成mid - eps，防止死循环；可能会错过极值，但在误差范围以内所以没关系
    else
        r = mid;
}

应用

一元函数求最值（三分法）

P3382 【模板】三分法

二元函数求最值（三分套三分）

P2571 [SCOI2010]传送带

代码

#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-10;
double ABx,ABy,CDx,CDy,P,Q,R;
double Ax,Ay,Bx,By,Cx,Cy,Dx,Dy;
double dis(double x1,double y1,double x2,double y2)
{
	return sqrt( (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2) );
}
double f(double x, double y)
{
	double Ax1=Ax+ABx*x,Ay1=Ay+ABy*x;
	double Dx1=Dx+CDx*y,Dy1=Dy+CDy*y;
	return dis(Ax,Ay,Ax1,Ay1)/P+dis(Ax1,Ay1,Dx1,Dy1)/R+dis(Dx,Dy,Dx1,Dy1)/Q;
}
double run(double x) // 固定x，三分y
{
	double l =0, r =1, mid;
	while (r - l > eps)
	{
		mid = (l + r) / 2;
		if (f(x, mid - eps) > f(x, mid + eps))
			l = mid;
		else
			r = mid;
	}
	return f(x, mid);
}
int main()
{
	cin>>Ax>>Ay>>Bx>>By>>Cx>>Cy>>Dx>>Dy;
	ABx=Bx-Ax,ABy=By-Ay;//A向B走
	CDx=Cx-Dx,CDy=Cy-Dy;//D向C走
	cin>>P>>Q>>R;
	double l = 0, r = 1, mid, ans;
	while (r - l > eps)
	{
		mid = (l + r) / 2; // 三分x
		double fl = run(mid - eps), fr = run(mid + eps);
		if (fl > fr)//求最小值把小于换成大于
			l = mid; // 这里不写成mid - eps，防止死循环；可能会错过极值，但在误差范围以内所以没关系
		else
			r = mid;
	}
	printf("%.2f\n", run(mid));
	return 0;
}

三分答案

没啥好说的