乘法逆元

定义

当 $ a*x ≡ 1\ ( mod\ p) $，且 $gcd(a,b)=1$,称 x 即为 a 在 mod p 意义下的逆元，记作 $inv(a,p)$。

简单理解：就是在求余意义下的倒数。如 $\frac{a}{b}\ mod\ c= a * inv(b) \ mod\ c$

求解

费马小定理（ p 为质数）

时间复杂度 $O(log\ p)$

数学证明

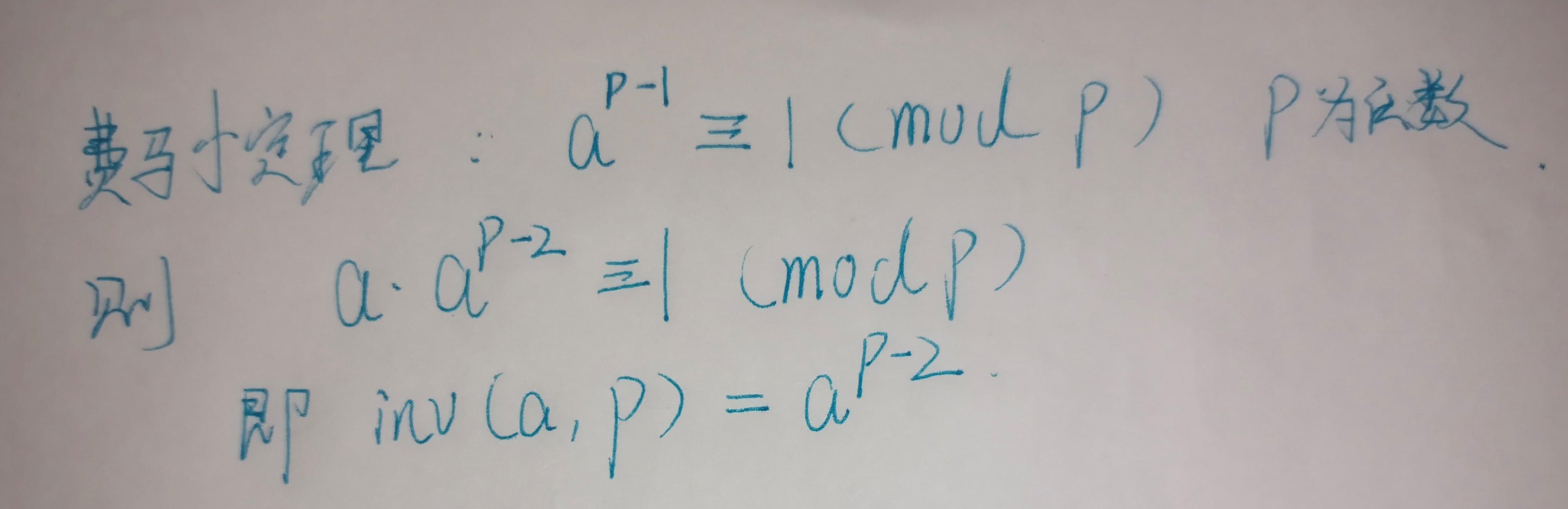
代码实现

typedef long long ll;
typedef unsigned long long ull;
typedef long double lb;
inline ll ksc(ull x,ull y,ll p) //O(1)快速乘（防爆long long）
{
	return (x*y-(ull)((lb)x/p*y)*p+p)%p;
}
inline ll fastPow(ll a,ll k,ll p)// a 底数， k 指数， 求 a^k mod p
{
	long long res = 1;
	a%=p;
	while(k > 0)
	{
		if (k & 1) res =ksc(res,a,p);
		a = ksc(a,a,p);
		k >>= 1;
	}
	return res;
}
ll gcd(ll a,ll b)
{
	if(b==0) return a;
	return gcd(b,a%b);
}
ll inv(ll a,ll p)
{
	if(gcd(a,p)!=1) return -1;//不符合费马小定理
	return fastPow(a,p-2,p);
}

拓展欧几里得（a，p 互质）

时间复杂度 $O(log\ n)$

数学证明

代码实现

long long ExGcd(long long a,long long b,long long& x,long long& y)
{
	if (b==0)
	{
		x=1;
		y=0;
		return a;
	}
	long long ans=ExGcd(b,a%b,x,y);	//先计算底层x y
	long long temp=y;
	y=x-(a/b)*y;
	x=temp;
	return ans;
}
long long inv(long long a,long long p)
{
	long long x,y;
	if(ExGcd(a,p,x,y)!=1) return -1;//不符合拓展欧几里得算法
	return (x%p+p)%p;//正数化 
}

线性算法( p 是质数)

时间复杂度 $O(log_2\ p)$

原理

代码实现

单次查询

int inv(int a,int p)//以费马小定理作为推导前提，所以 p 需要是质数
{
	if(a==1) return 1;
	return -(p/a)*inv(p%a,p)%p;
}

多次查询

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e7+7;
long long inv[maxn];
int main()
{
	ios::sync_with_stdio(false);
	long long n,p;
	cin>>n>>p;
	inv[1]=1;
	cout<<inv[1]<<endl;
	for(int i=2; i<=n; ++i)
	{
		inv[i]=(long long)(p-p/i)*inv[p%i]%p;
		cout<<inv[i]<<'\n';
	}
	return 0;
}