题目链接
题意分析
- C 数组中存放点的权值(从小到大排序)
边的权值
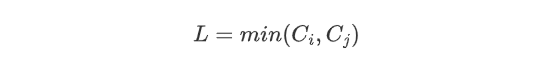
C[i] C[j]为 L 的两个端点值
易知C[1]相连的边,其权值均为C[1]
由贪心策略易知,越权值小的点,其相连边权值越小,因此应尽量减少其相连边,理想情况为将其填入叶子节点中。
样例分析
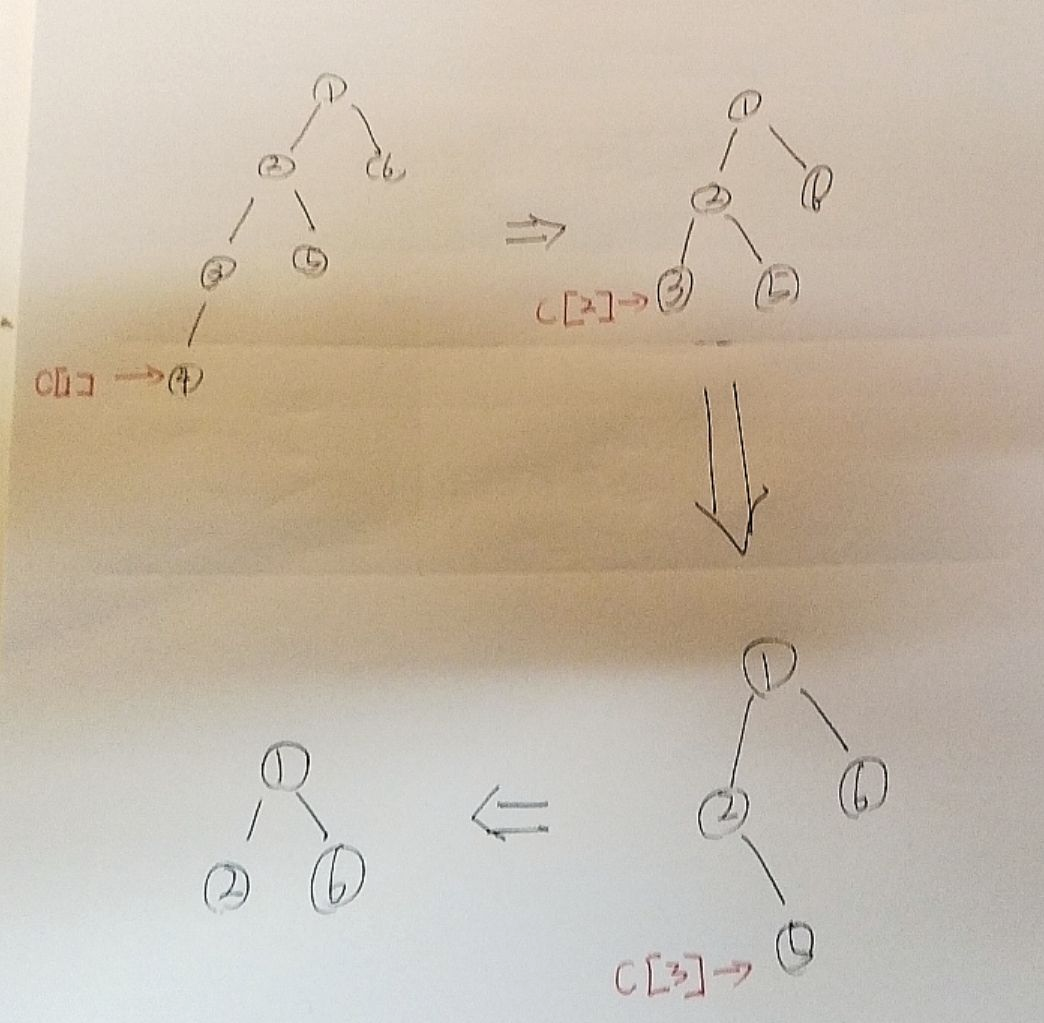
如图所示,在 4 号节点填入 C[1] 后,3-4 这条边已经确定权值了,我们可以将它删去,则 3 号节点成为了一个新的叶子节点
在 3 号节点填入 C[2] 后,3-2 这条边已经确定权值了,我们可以将它删去
在 5 号节点填入 C[3] 后,5-2 这条边已经确定权值了,我们可以将它删去
后续操作不进行赘述。
基于上述操作方法,我们做到每一个当前情况下的最小点,均填入当前情况下的叶子节点中,从而使边权值最大。
结论
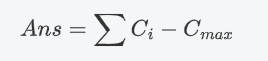
即每个点(除了最大点)的值均为一条边的权值。
要满足这个情况只需要使:只要子节点的值小于父节点的值即可
代码实现
BFS

//采用按层填充
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+7;
int C[maxn],N,Ans,ans[maxn];
vector <int> T[maxn];
void BFS(int root)
{
queue<int>Q;
int cnt=N;
int l=T[root].size();
for(int i=0; i<l; ++i)
{
Q.push(T[root][i]);
}
ans[root]=C[cnt--];
while(!Q.empty())
{
root=Q.front();
Q.pop();
if(ans[root]) continue;
ans[root]=C[cnt--];
l=T[root].size();
for(int i=0; i<l; ++i)
{
Q.push(T[root][i]);
}
}
}
int main()
{
int a,b;
cin>>N;
for(int i=1; i<=N-1; ++i)
{
cin>>a>>b;
T[a].push_back(b);
T[b].push_back(a);
}
for(int i=1; i<=N; ++i)
{
cin>>C[i];
Ans+=C[i];
}
sort(C+1,C+1+N);
Ans-=C[N];//最大值计算
BFS(1);
cout<<Ans<<endl;
for(int i=1; i<=N; ++i)
{
cout<<ans[i]<<" ";
}
return 0;
}DFS
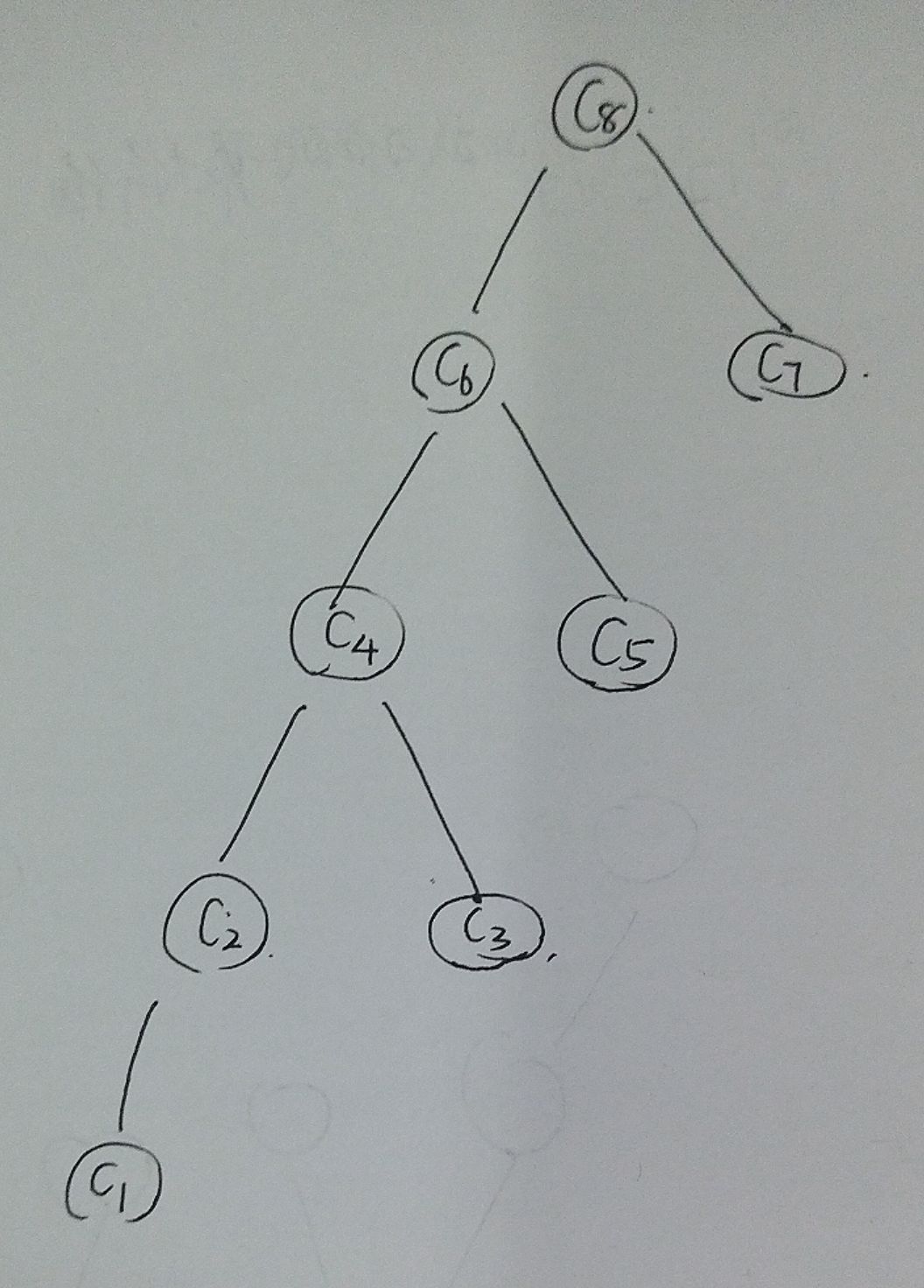
//仿照后序遍历的方式进行节点填充
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+7;
int C[maxn],N,Ans,ans[maxn],cnt,vis[maxn];
vector <int> T[maxn];
void DFS(int root)
{
vis[root]=1;
for(int i=0; i<T[root].size(); ++i)
{
int v=T[root][i];
if(vis[v]) continue;
DFS(v);
}
ans[root]=C[++cnt];
Ans+=ans[root];
}
int main()
{
int a,b;
cin>>N;
for(int i=1; i<=N-1; ++i)
{
cin>>a>>b;
T[a].push_back(b);
T[b].push_back(a);
}
for(int i=1; i<=N; ++i)
cin>>C[i];
sort(C+1,C+1+N);
DFS(1);
cout<<Ans<<endl;
for(int i=1; i<=N; ++i)
{
cout<<ans[i]<<" ";
}
return 0;
}
