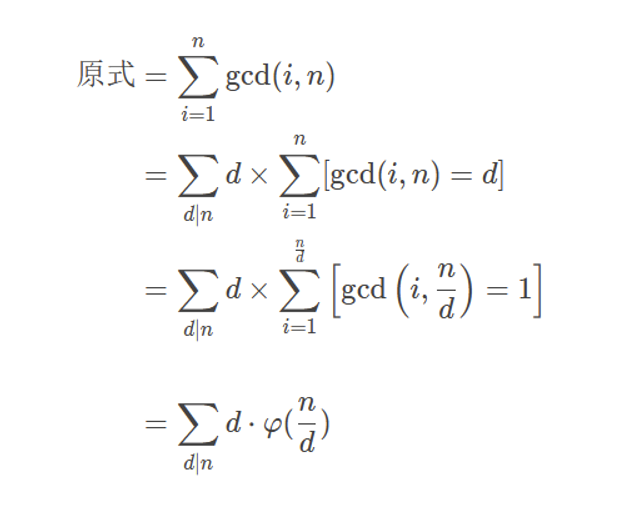原理简介
欧拉函数:对正整数 n ,欧拉函数是小于等于 n 的数中与 n 互质的数的数目
性质
- 若 a 为质数,则 $ ψ(a)=a−1$
- 若 a,b 互质,则 $ψ(a∗b)=ψ(a)*ψ(b)$ (欧拉函数是积性函数)
- 若 b 为 a 的倍数,则 $ ψ(ab)=a*ψ(b)$
- 若 p 为素数,则 $ψ(p^a)=(p-1)*p^{a-1}$
- 由 3 可得:设 $n=p_1^{a_1} p_2^{a_2} ··· p_n^{a_n}$ 为正整数 n 的素数幂乘积表达式,则 $ψ(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})*···$
代码实现
单个求解
long long euler(long long n)//欧拉函数
{
long long ans=n;
for(long long i=2;i*i<=n;++i)
if(n%i==0)
{
ans=ans-ans/i;
while(n%i==0) n/=i;
}
if(n>1) ans=ans-ans/n;
return ans;
} 连续求解($O(n*ln\ ln\ n )$)
const long long maxn=1e6+7;
long long f[maxn];//f[i]指 ψ(i)
long long p[maxn],cnt;//p[i]用于存储第i格质数,cnt用于统计素数个数
long long tag[maxn];//tag[i] 用于记录i是否是素数
void euler(long long n)//线性筛选素数,求出 2-n 的所有欧拉函数值
{
f[1]=1;
for(long long i=2; i<=n; ++i)
{e
if(!tag[i])
{
p[++cnt]=i;
f[i]=i-1;//若 a 为质数,则ψ(a)=a-1
}
for(long long j=1; j<=cnt&&i*p[j]<=n; j++)
{
long long v=i*p[j];
tag[v]=1;
if(i%p[j]==0)
{
f[v]=f[i]*p[j];//性质3 若 b 为 a 的倍数,则 ψ(a*b)=a*ψ(b)
break;
}
//p[j]的因数只有1和它本身,所以p[j]与i互质,符合性质2
f[v]=f[i]*f[p[j]];//性质2
}
}
}应用场景
1. gcd 求和