定义
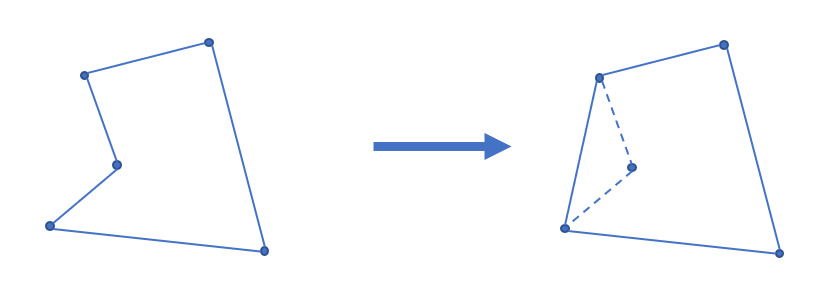
凸包就是求一个周长最小的,并且能包围所有给定点的多边形。当多边形表面存在凹陷时,根据三角不等式$\begin{cases}
a+b>c\
b+c>a\
a+c>b\
\end{cases}$,一定没有直接把最短那条边连起来优。
解决算法
算法挺多的,时间不太够,先学一个。
Grajam-Scan
Graham扫描法的原理是从点集中先找出一个最左下方的点,可以证明,这个点肯定在凸包上(易证),然后以这个点为极点,将所有点根据与这个点的极角排序,并且同时使用一个栈结构维护凸包上的点。
算法步骤
- 选出 x 坐标最小的点作为极点(x坐标相同,选y最小的点)。这个点必在凸包上。
- 将其余点按极角排序,在极角相同的情况下比较与极点的距离,离极点比较近的优先。
- 用一个栈S存储凸包上的点,先将按极角和极点排序最小的两个点入栈。
- 按需扫描每个点,检查栈顶的前两个元素与这个点构成的折线段是否“拐”向右侧 (叉积[1])。、
- 如果满足,则弹出栈顶元素,并返回 4再次检查,直至不满足。将该点入栈,并对其他点不断执行 5 操作。
- 最终栈中的元素为凸包的顶点序列。
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+7;
const double EPS=1e-8;//最低要求是高于题目要求精度
struct Point
{
double x,y;
Point(double _x=0,double _y=0)
{
x=_x;
y=_y;
}
friend Point operator +(const Point &a,const Point &b)
{
return Point(a.x+b.x,a.y+b.y);
}
friend Point operator -(const Point &a,const Point &b)
{
return Point(a.x-b.x,a.y-b.y);
}
friend double operator ^(const Point &a,const Point &b)
{
return a.x*b.y-a.y*b.x;//叉乘
}
};
Point Dots[maxn];
Point stk[maxn];
struct V
{
Point start,end;
double ang;//偏角
V(Point _start=Point(0,0),Point _end=Point(0,0),double _ang=0.0)//初始化
{
start=_start;
end=_end;
ang=_ang;
}
friend V operator +(const V &a,const V &b)
{
return V(a.start+b.start,a.end+b.end);//使用默认列表初始化,因此可以只使用两个参数
}
friend V operator -(const V &a,const V &b)
{
return V(a.start-b.start,a.end-b.end);//使用默认列表初始化,因此可以只使用两个参数
}
};
struct Circle
{
double r;
Point centre;
Circle(Point _centre=Point(0,0),double _r=0)
{
centre=_centre;
r=_r;
}
};
long long n,top;//n 点的个数
double Distance(const Point &a,const Point &b)
{
//可能出问题
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double Parellel(double key)
{
return fabs(key)<EPS?0:key;
}
int cmp(const Point &a,const Point &b)
{
double res=Parellel((a-Dots[1])^(b-Dots[1]));
if(res>0) return 1;
if(res==0&&Distance(a,Dots[1])<Distance(b,Dots[1])) return 1;
return 0;
}
void Graham()
{
sort(Dots+2,Dots+1+n,cmp);
top=2;
stk[1]=Dots[1];
stk[2]=Dots[2];
for(int i=3; i<=n; ++i)
{
while(top>=2&&((stk[top]-stk[top-1])^(Dots[i]-stk[top-1]))<EPS) --top;
stk[++top]=Dots[i];
}
stk[top+1]=stk[1];
}
int main()
{
cin>>n;
for(int i=1; i<=n; ++i) cin>>Dots[i].x>>Dots[i].y;
int k=1;//最左下角的点的编号
for(int i=2; i<=n; ++i)
{
if(Dots[i].x<Dots[k].x||((Dots[i].x-Dots[k].x<EPS)&&Dots[i].y<Dots[k].y))
{
k=i;
}
}
swap(Dots[1],Dots[k]);// 使第一个点为最左下角的点
Graham();
double ans=0;
for(int i=1; i<=top; ++i)//完成后stk中就是凸包的所有顶点按逆时针存放
{
ans+=Distance(stk[i],stk[i%top+1]);
}
printf("%.2lf",ans);
return 0;
}
- 1.链接 ↩
![P3829 [SHOI2012]信用卡凸包](/medias/featureimages/3.jpg)
