题目链接
题目分析
由于本题的最难点就在于对圆角的处理,因此直接切入正题。
如图所示
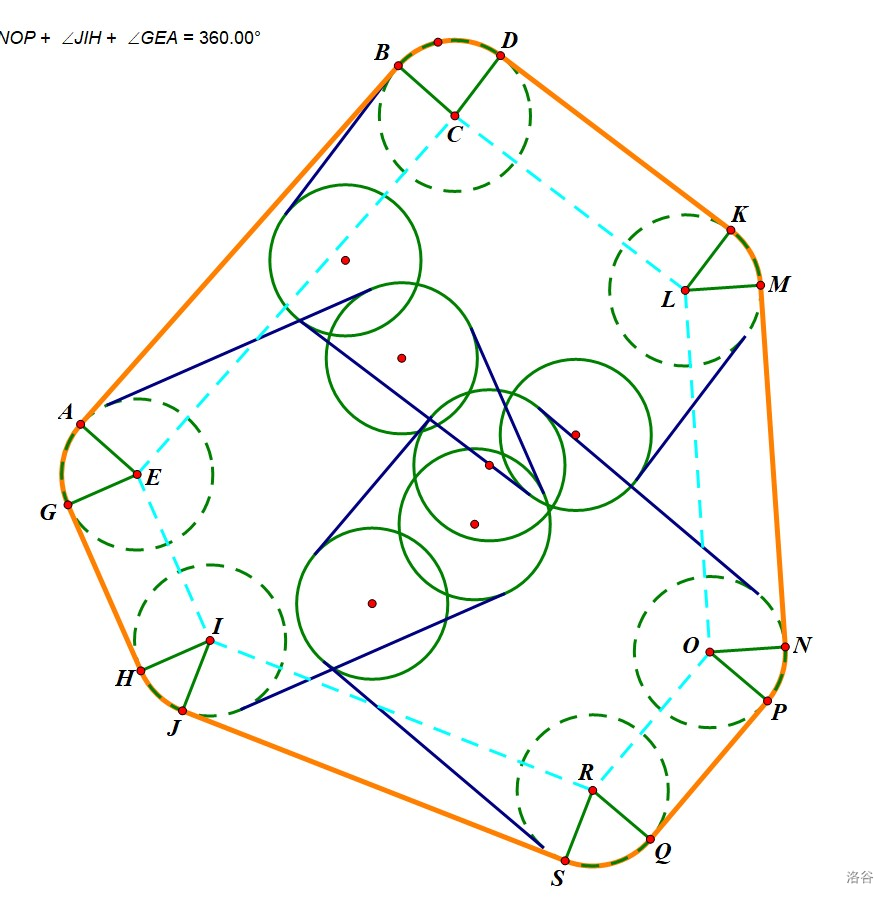
不难发现其周长为 $凸包长度+\overset{\LARGE{\frown}}{BD}+\overset{\LARGE{\frown}}{KM}+\overset{\LARGE{\frown}}{NP}+\overset{\LARGE{\frown}}{SQ}+\overset{\LARGE{\frown}}{HJ}+\overset{\LARGE{\frown}}{GA}$,单独计算每个弧线,其计算难度稍大。因此我们不妨改变一个思路,计算单个有难度,直接计算和怎么r样?
直接计算和就很简单了,可以发现这是一个闭合图形,直线不改变方向,弧线改变方向,最终形成闭环就代表所有的弧线组成一个圆。
因此最终的周长就是$凸包长度+2πr$
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> Pair;
const int maxn=1e6+7;
const double EPS=1e-6;//必须比题目给出的精度高
const double pi = 3.141592653589793;
struct Point
{
double x,y;
Point(double _x=0,double _y=0)
{
x=_x;
y=_y;
}
friend Point operator +(const Point &a,const Point &b)
{
return Point(a.x+b.x,a.y+b.y);
}
friend Point operator -(const Point &a,const Point &b)
{
return Point(a.x-b.x,a.y-b.y);
}
friend double operator ^(const Point &a,const Point &b)
{
return a.x*b.y-a.y*b.x;//叉乘
}
};
Point Dots[maxn];
Point stk[maxn];
map<Pair,int>number;
struct V
{
Point start,end;
double ang;//偏角
V(Point _start=Point(0,0),Point _end=Point(0,0),double _ang=0.0)//初始化
{
start=_start;
end=_end;
ang=_ang;
}
friend V operator +(const V &a,const V &b)
{
return V(a.start+b.start,a.end+b.end);//使用默认列表初始化,因此可以只使用两个参数
}
friend V operator -(const V &a,const V &b)
{
return V(a.start-b.start,a.end-b.end);//使用默认列表初始化,因此可以只使用两个参数
}
};
struct Circle
{
double r;
Point centre;
Circle(Point _centre=Point(0,0),double _r=0)
{
centre=_centre;
r=_r;
}
};
long long n,top;//n 点的个数
double Distance(const Point &a,const Point &b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double Parellel(double key)
{
return fabs(key)<EPS?0:key;
}
int cmp(const Point &a,const Point &b)
{
double res=Parellel((a-Dots[1])^(b-Dots[1]));
if(res>0) return 1;
if(res==0&&Distance(a,Dots[1])<Distance(b,Dots[1])) return 1;
return 0;
}
void Graham()
{
sort(Dots+2,Dots+1+n,cmp);
top=2;
stk[1]=Dots[1];
stk[2]=Dots[2];
for(int i=3; i<=n; ++i)
{
while(top>=2&&((stk[top]-stk[top-1])^(Dots[i]-stk[top-1]))<EPS) --top;
stk[++top]=Dots[i];
}
stk[top+1]=stk[1];
}
int main()
{
cin>>n;
double a,b,c,r,x,y,ang1,ang2;//ang1是矩形的长宽比角,ang2是偏转角
cin>>a>>b>>r;
a-=2*r;
b-=2*r;
c=sqrt(a*a+b*b)/2;
ang1=atan(a/b);
n*=4;
for(int i=1; i<=n; i+=4)//存入四个圆心
{
cin>>x>>y>>ang2;
Dots[i]=Point(x-c*cos(ang1-ang2),y+c*sin(ang1-ang2));
Dots[i+1]=Point(x+c*cos(ang1+ang2),y+c*sin(ang1+ang2));
Dots[i+2]=Point(x+c*cos(ang1-ang2),y-c*sin(ang1-ang2));
Dots[i+3]=Point(x-c*cos(ang1+ang2),y-c*sin(ang1+ang2));
}
int k=1;//最左下角的点的编号
for(int i=2; i<=n; ++i)
{
if(Dots[i].x<Dots[k].x||(Dots[i].x-Dots[k].x<EPS&&Dots[i].y<Dots[k].y))
{
k=i;
}
}
swap(Dots[1],Dots[k]);// 使第一个点为最左下角的点
Graham();
double ans=0;
for(int i=1; i<=top; ++i)//完成后stk中就是凸包的所有顶点按逆时针存放
{
ans+=Distance(stk[i],stk[i%top+1]);
}
ans+=2*pi*r;
printf("%.2lf",ans);
return 0;
}
//注意数据范围

